UNIÓN DE CONJUNTOS
La unión de los conjuntos A y B es el conjunto formado por todos los elementos que pertenecen a A o a B o a ambos. Se denota: A U B. La unión de conjuntos se define como:
A U B = {x / x 
A o x B}
comentario:
en si la union de conjuntos es la union de los elementos de dos conjuntos distintos.
Intersección
Los elementos comunes a 
y 
forman un conjunto denominado intersección de y , representado por 
. Es decir, es el conjunto que contiene a todos los elementos de A que al mismo tiempo están en B:
.
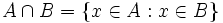Si dos conjuntos y son tales que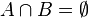 
, entonces y se dice que son conjuntos disjuntos.
Es claro que el hecho de que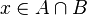 
es condición necesaria y suficiente para afirmar que 
y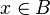 
. Es decir
Ejemplos: si tenemos los conjuntos
en si es la separacion de l0s elementos que se repiten entre dos conjuntos es decir los elementos que los contenga a y b se separan y se ubican en la parte intermedia.
Diferencia
Los elementos de un conjunto que no se encuentran en otro conjunto , forman otro conjunto llamado diferencia de y , representado por 
. Es decir:
.
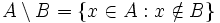o dicho de otra manera:
Algunas personas prefieren denotar la diferencia de 
y 
como 
.
Una propiedad interesante de la diferencia es que
eso es porque
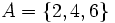
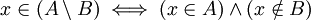
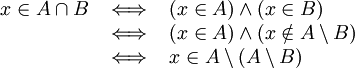
No hay comentarios:
Publicar un comentario