Esperanza matemática
En estadística la esperanza matemática (o simplemente esperanza) o valor esperado de una variable aleatoria es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso. Por ejemplo, en un juego de azar el valor esperado es el beneficio medio.
Si todos los sucesos son de igual probabilidad la esperanza es la media aritmética.
Definición [editar]
Para una variable aleatoria discreta con valores posibles 
y sus probabilidades representadas por la función de masa p(xi) la esperanza se calcula como:
![E[X]=\sum_{i=1}^{n} x_i p(x_i) \,\!](http://upload.wikimedia.org/math/a/3/1/a314743e00cbe03ed42a3b5c93aeea12.png)
Para una variable aleatoria continua la esperanza se calcula mediante la integral de todos los valores y la función de densidad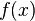 
:
![E[X]=\int_{-\infty}^\infty x f(x)dx \,\!](http://upload.wikimedia.org/math/0/1/e/01ee197ad5dbb61b90d3ed7de412f720.png)
- o
![\operatorname{E}[X] = \int_\Omega X\, \operatorname{d}P \,\!](http://upload.wikimedia.org/math/2/b/b/2bb82da2aad67daf5519781e29dc4016.png)
La esperanza también se suele simbolizar con ![\mu = E[X] \,\!](http://upload.wikimedia.org/math/3/2/7/3279ba1ddb2ac80fce25a62bee4a55f4.png)
Las esperanzas ![E[X^k] \,\!](http://upload.wikimedia.org/math/f/7/1/f71df20458573663d1d38537e4e2b082.png)
para 
se llaman momentos de orden 
. Más importantes son los momentos centrados ![E[(X-E[X])^k] \,\!](http://upload.wikimedia.org/math/a/1/2/a1293ec70351b19f815480e7e2c63840.png)
.
No todas las variables aleatorias tienen un valor esperado. Por ejemplo, la distribución de Cauchy no lo tiene.
comentario: la esperanza matematica esta relacionada con lo que es el valor aleatorio de una variable
